深度篇——神经网络(五) 细说 优化器

发布时间：2024-07-01 13:22:34 丨 文章作者：佚名 丨 浏览次数：103

返回主目录

返回神经网络目录

上一章：深度篇——神经网络(四)  细说 调优神经网络

下一章：深度篇——神经网络(六)  细说 数据增强与fine-tuning

 

本小节，细说 优化器，下一小节细说 数据增强与fine-tuning

对优化器的选择，包括后面的数据增强与fine-tuning，也都属于对神经网络的调优过程。

 

5. 调优神经网络

(9). 优化器

优化器示图：

 

a. BGD (Batch Gradient Descent, BGD) 批量梯度下降法

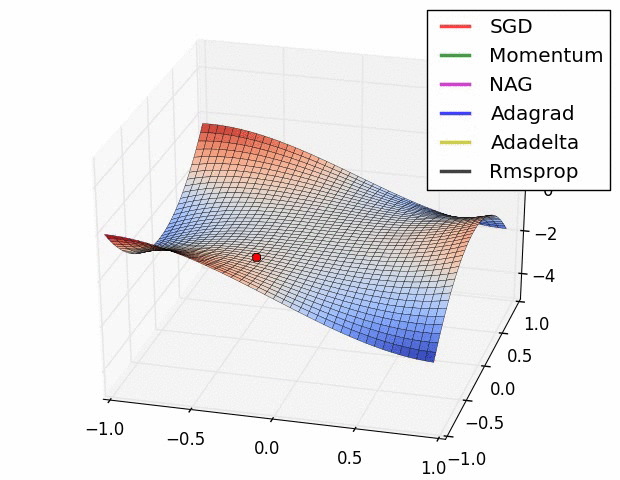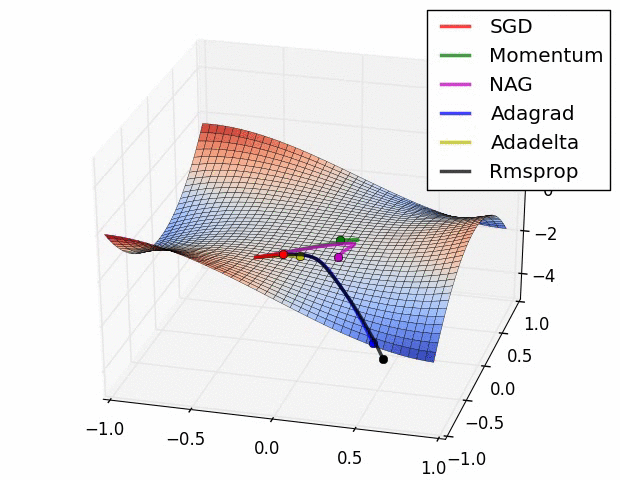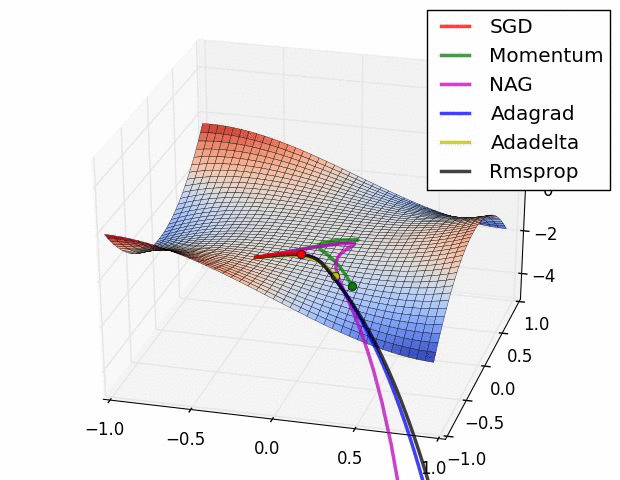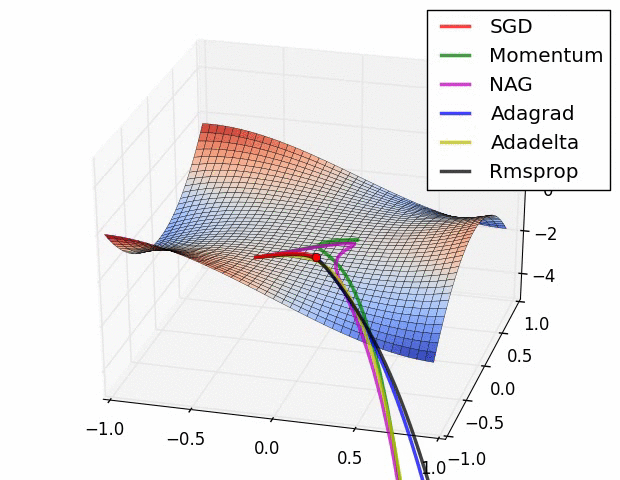
    BGD 采用整个训练集的数据  来计算 cost function 和 参数的梯度：

                 

                 ：为所有样本的梯度

     优点：

            对于凸函数可以收敛到全局极小值，对于非凸函数可以收敛到局部极小值

     缺点：

            由于这种方法是在一次更新中，就对整个数据集计算梯度，所以计算起来非常慢，遇到很大量的数据集也会非常棘手，而且不能投入新数据实时更新模型。

 

b. SGD (Stochastic Gradient Descent, SGD) 随机梯度下降法

    SGD 随机梯度下降更新时针对每一个样本集  和 。

    BGD 在数据量很大时会产生大量冗余的计算，而 SGD 每次只更新一个，因此 SGD 算法通常更快，并且适合 online，可以新增样本。

                

                ：为样本  的梯度。

     优点：

            SGD 的震荡可能会跳到更好的局部极小值处，从而获得更好的局部最优解。

     缺点：

            SGD 因为更新比较频繁，容易造成 cost function 严重的震荡。

 

c. MBGD (Mini Batch Gradient Descent, MBGD) 小批量梯度下降法

   MBGD 小批量梯度下降法，每次利用一小批样本，即 m 个样本进行计算。这样它可以降低参数更新时的方差，收敛更稳定。可以充分利用深度学习库中高度优化的矩阵来进行更有效的梯度计算。

                 

                 ：为小批量样本数，一般取值在 50 ~ 2 56

                 ：为第  到  个样本的梯度

     优点：

            减少了参数更新的变化，这可以带来更加稳定的收敛。

            可以充分利用矩阵优化，最终计算更加高效

     缺点：

            不能保证很好的收敛。

 

d. BGD，SGD，MBGD 算法都需要预先设置学习率，学习率的设置，往往会带来一些问题：

   (a). 选择一个合适的学习率是非常困难的事。如果整个模型计算过程中都采用相同的学习率进行计算：如果学习率太小，收敛速度将会很慢，并且容易困在并不怎么理想的局部最优解处。而学习率较大时，收敛过程将会变得非常抖动，而且有可能不能收敛到最优。

   (b). 有一种措施是先设定大一点的学习率，当两次迭代之间变化低于某个阈值后，就减少学习率。不过需要提前设定好阈值和减小学习率的规则

   (c). 当数据非常稀疏的时候，可能不希望所有数据都以相同的方式进行梯度更新，而是对这种极少的特征进行一次大的更新

   (d).对于非凸函数，关键的挑战是要避免陷于局部极小值处，或者鞍点处，因为鞍点周围的 error 都是一样的，所有维度的 梯度都接近于 零， SGD 特别容易被困在此处。 

 

e. Momentum 动量法

     momentum 是模型里动量的概念，积累之前的动量来替代真正的梯度。公式如下：

                

                

                

                ：为 梯度

                ：为  时刻的速度(变化量)

                ：为动量因子，一般常取 0.9

                ：为学习率

      通过添加一个衰减因子到历史更新向量，并加上当前的更新向量。当梯度保持相同方向时，动量因子加速参数更新；而梯度方向改变时，动量因子能降低梯度的更新速度。

     优点：

            下降初期时，使用上一次参数更新，下降方向一致，乘上较大的  能够进行很好的加速。

            下降中后期时，在局部最小值来回震荡的时候，梯度  趋近于 零，